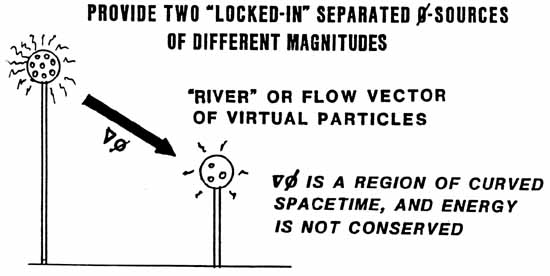
Now if we wish to get free energy, we are going to have to provide a continuous anenergy river, and a means of tapping it to produce mass movement. 
          This slide shows one easy way to make an anenergy river. 
          We simply pump some electrons (spray nozzles) onto an elevated charged ball, and we LEAVE them there.  A second ball is connected to ground.  A higher phi -- that is, a denser spray -- is now in the vicinity of the elevated ball on the left.  A lower phi -- that is, a less dense spray -- is in the vicinity of the lower ball on the right.  Between the two balls, now, there is a gradient in phi, and a virtual flux flowing from the "higher virtual pressure" to the "lower virtual pressure."
          This del-phi river does NOT constitute an Ë-field, as we
have previously pointed out. 
          The del-phi region, however, is definitely a region of
curved spacetime.  As is well known from general relativity, in such a region energy need not be conserved. 
          Therefore it is entirely possible -- consistent with ordinary physics -- to violate conservation of energy in this del-phi river, if one believes general relativity.  If one argues adamantly that conservation of energy cannot be violated under any circumstances, then one must throw out general relativity.  Also, one must throw out most of particle physics, whose explanations presently involve virtual interactions, each of which violates the conservation of energy. 

Next Slide